Armaduras mínimas en elementos de hormigón armado

Calculo de estructura de tribuna

Datos de entrada
hormigón T m

Tipos de barra b  h
1 0.3  0.7 r   ,   2 0.4  0.8  r ,   3 0.3  0.6 ra

(El tipo de barra es un número que la identifica, en este caso hay tres tipos, el numero 1 es una barra rectangular (r) de sección 30x70 cmxcm.; empotrada por sus dos extremos. La barra numero 3 también es rectangular pero tiene dos articulaciones en sus extremos)

Nudos: Numero ABSCISA  y ORDENADA
 1  0.00 0.00   ,    2  5 0.00   ,    3 13.00  0.00
 4  0.00 4.00   ,    5  5 5.92   ,    6 10.02  7.85
 7 13.00 6.01   ,    8 13 9.00   ,    9 -1.00 14.40
10  4.00 13.80   ,   11 13 13

(Cada nudo se identifica por tres números separados del siguiente nudo por una coma, el primero es el numero del nudo seguido del valor de la abscisa o distancia horizontal al nudo 1, que sera siempre el 1 0 0, y el tercer numero es la ordenada del mudo o altura respecto del nudo 1)

Barra: i j Tipo de barra
 1  4  1   ,    2  5  1   ,    3  7  1   ,    4  5  2
 5  6  2   ,    6  8  2   ,    7  8  1   ,    6  7  2
 5 10  3   ,    8 11  1   ,    9 10  2   ,   10 11  2



(Cada grupo de datos, separados por comas, se compone de tres datos, los dos primeros son los números que indentifican los nudos extremos de cada barra y el tercer dato es el tipo de nudo según se indico antes)

APOYOS: nudo y coeficientes de Coacción
 1    0   0   0,    2    0   0   0,    3    0   0   0


(Cada grupo de cuatro datos corresponde a un nudo de apoyo de la estructura. El primero es el número del nudo y después las tres coacciones a que sometemos el nudo.)

Fuerzas en NUDOS
hipótesis 1
 8  3 0 0   ,   11  3 0 0

(Las fuerzas en los nudos se indican con el numero del nudo y la fuerza horizontal, que en el nudo 8 es de 3 en dirección de izquierda a derecha, en caso de ser de derecha a izquierda seria negativo, después la fuerza vertical y el momento flector aplicado al nudo)

hipótesis 2

(En la hipótesis 2 no hemos considerado ninguna fuerza en los nudos)

CARGAS en BARRAS
hipótesis 1
4   5,    10   0   0  270
5   6,    10   0   0  270
6   8,    10   0   0  270
9  10,     4   0   0  270
10 11,     4   0   0  270
hipótesis 2
4   5 ,  11.52   0   5.39  270
5   6 ,  11.52   0   5.34  270
6   8 ,  11.52   0   3.20  270
9  10 ,   3.84   0   5.03  270
10 11 ,   3.84   0   9.04  270

Resultados

CALCULO DE DESPLAZAMIENTOS, MOMENTOS, CORTANTES Y AXILES:
Nudos Barras Difmax  Hipot. Mod.Young  Uni.e.Fuer  Uni.e.Lon.
11      12      5      2  kg/cm2  2.4e6 T   1.000  m   1.000

                             HIPÓTESIS NUM.1
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
      Coordenadas       DESPLAZAMIENTOS DE NUDOS              Fuerzas en nudos
 Nudo   x       y    Direc. x  Direc. y         Giro         Fx     Fy      Mf
        m.      m.    m.          m.         rad.  Grados      T.     T.   m.T.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
 1     0.00    0.00  0.00000   0.00000   0.00000    0.000    0.00  0.00    0.00
 2     5.00    0.00  0.00000   0.00000   0.00000    0.000    0.00  0.00    0.00
 3    13.00    0.00  0.00000   0.00000   0.00000    0.000    0.00  0.00    0.00
 4     0.00    4.00  0.00058  -0.00016   0.00054    0.031    0.00  0.00    0.00
 5     5.00    5.92  0.00108  -0.00145   0.00073    0.042    0.00  0.00    0.00
 6    10.02    7.85  0.00231  -0.00494  -0.00103   -0.059    0.00  0.00    0.00
 7    13.00    6.01  0.00487  -0.00061  -0.00106   -0.061    0.00  0.00    0.00
 8    13.00    9.00  0.00071  -0.00078  -0.00174   -0.100    3.00  0.00    0.00
 9    -1.00   14.40 -0.00876  -0.01511  -0.00287   -0.164    0.00  0.00    0.00
10     4.00   13.80 -0.00736  -0.00336  -0.00080   -0.046    0.00  0.00    0.00
11    13.00   13.00 -0.00706  -0.00087  -0.00179   -0.103    3.00  0.00    0.00


                             HIPÓTESIS NUM.1
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
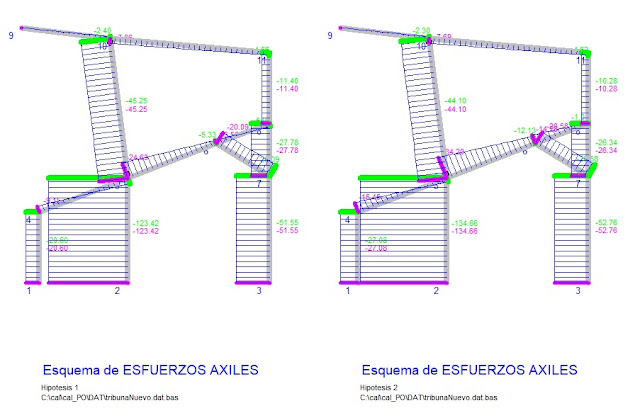
                                ESFUERZOS EN BARRAS
 i  j tB    Axil i  Corte.i    Momto.i    Axil j  Corte.j    Momto.j  m.centro  i  j
                T.      T.       m.T.        T.         T.       m.T.       m.T.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
 1  4  1   -20.60C     1.89       1.01   -20.60C     1.89       6.54   2.76  1  4
 2  5  1  -123.42C     1.29       1.27  -123.42C     1.29       6.35   2.54  2  5
 3  7  1   -51.55C    -9.17     -23.93   -51.55C    -9.17     -31.20  -3.63  3  7
 4  5  2    -9.15C   -18.55      -6.54    10.05C    31.45      41.06  -9.68  4  5
 5  6  2   -24.63C   -39.36     -47.40    -5.33C    10.84     -29.27 -24.68  5  6
 6  8  2    -5.55C   -14.54       1.75     5.95C    15.26      -0.60 -13.07  6  8
 7  8  1   -27.78C    -0.24       4.33   -27.78C    -0.24      -5.05  -4.69  7  8
 6  7  2   -20.09C    15.53      27.53   -20.09C    15.53      26.87  -0.33  6  7
 5 10  3   -45.25C     0.00       0.00   -45.25C     0.00       0.00   0.00  5 10
 8 11  1   -11.40C     2.70       5.65   -11.40C     2.70       5.14  -0.26  8 11
 9 10  2     0.00C     0.00       0.00    -2.40C    20.00      50.36  12.59  9 10
10 11  2     7.86T   -24.14     -50.36     4.66T    11.86      -5.14 -18.05 10 11

Hipotesis 1
 i   j sen(a) cos    a.a    L   Area    Iner   Vol      Peso   b  h
                   grados   m.   cm²     cm4   m.³       T.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
 1  4 -1.00  0.00  -90.00  4.00 2100  857500  0.84     2.02 r 30 70
 2  5 -1.00  0.00  -90.00  5.92 2100  857500  1.24     2.98 r 30 70
 3  7 -1.00  0.00  -90.00  6.01 2100  857500  1.26     3.03 r 30 70
 4  5 -0.36 -0.93  -21.01  5.36 3200 1706667  1.71     4.11 r 40 80
 5  6 -0.36 -0.93  -21.03  5.38 3200 1706667  1.72     4.13 r 40 80
 6  8 -0.36 -0.93  -21.10  3.19 3200 1706667  1.02     2.45 r 40 80
 7  8 -1.00  0.00  -90.00  2.99 2100  857500  0.63     1.51 r 30 70
 6  7  0.53 -0.85   31.69  3.50 3200 1706667  1.12     2.69 r 40 80
 5 10 -0.99  0.13  -82.77  7.94 1800       0  1.43     3.43 ra 30 60
 8 11 -1.00  0.00  -90.00  4.00 2100  857500  0.84     2.02 r 30 70
 9 10  0.12 -0.99    6.84  5.04 3200 1706667  1.61     3.87 r 40 80
10 11  0.09 -1.00    5.08  9.04 3200 1706667  2.89     6.94 r 40 80
                                             ¯¯¯¯¯¯¯¯¯¯¯¯¯¯
                                             16.32    39.18


Hipotesis 1
Caracteristicas de los materiales
Hormigon  fck=  25 N/mm2   fcd = fck*100*0.9/cSh =   1500 T/m2
Acero HA  fyk= 500 N/mm2   fyd = fyk*100/cSa     =  43478 T/m2
-----------------------------------------------------------------------------
    Pilar con armadura simetrica en los cuatro lados
mu=M/b/h^2/fcd   v=N/b/h/fcd   w = (a1+a2*mu)/(1-a3*delta) r=40 mm
Area minima = 4*b*h/1000   area=fcd*w*b*h/fyd
Jacenas: U=0.85*fcd*b*d    v=U*d*0.375

 i  j  bxh       N    M    mu     v     x.a   a1   a2   a3     w     Area dis
      cm cm      T   mT                                               cm2  cm
 i  j                      U      v    UT     UC       aT     aC    nrT    nrC
              _____________
______________________________________________________________________________
10 11 40 80    12.6 68.5  387.6 110.9 104.09   0.00  28.73   0.00 15Ø16
               12.6  7.0                9.30   0.00   6.72   0.00  4Ø16
               12.6 33.2               46.48   0.00  12.83   0.00  7Ø16

 9 10 40 80     3.8  0.0  387.6 110.9   0.00   0.00   6.72   0.00  4Ø16
                3.8 68.5              104.09   0.00  28.73   0.00 15Ø16
                3.8 23.2               31.78   0.00   8.77   0.00  5Ø16
 8 11 30 70    18.2  9.0  0.065 0.092  91.9 -0.16 2.54 2.03 0.01 8.40~       11 8Ø12
 5 10 30 60    72.4  1.6  0.036 0.976  75.9 -0.09 2.91 1.99 0.02 7.20~ª2.2   11 8Ø12
 6  7 40 80    32.1 37.4  387.6 110.9  52.86   0.00  14.59   0.00  8Ø16
               32.1 36.5               51.50   0.00  14.22   0.00  8Ø16
               32.1  0.6                0.80   0.00   6.72   0.00  4Ø16
 7  8 30 70    44.4  8.1  0.058 0.224  24.0 -0.25 2.67 2.14  -0.11   8.40~   11  8Ø12
 6  8 40 80     9.5  2.8  0.012 0.032  31.5 -0.25 2.67 2.14  -0.25  12.80~   13 10Ø14
 5  6 40 80    39.4 64.5  387.6 110.9  96.96   0.00  26.76   0.00 14Ø16
               39.4 39.8               56.50   0.00  15.59   0.00  8Ø16
               39.4 45.4               65.25   0.00  18.01   0.00  9Ø16

 4  5 40 80    16.1  8.9  387.6 110.9  11.88   0.00   6.72   0.00  4Ø16
               16.1 55.8               82.19   0.00  22.68   0.00 12Ø16
               16.1 18.5               25.13   0.00   6.94   0.00  4Ø16
 3  7 30 70    82.5 49.9  0.534 0.618  18.0 -0.28 2.76 2.37   1.38
      35 75               0.372 0.461  61.5 -0.32 2.75 2.27   0.80  45.55  ª1.39  6 18Ø20
 2  5 30 70   197.5 10.2  0.107 1.458
      35 75               0.075 1.088  88.4 -0.02 3.01 1.69   0.23  13.01  ª1.37 11 10Ø14
 1  4 30 70    33.0 10.5  0.075 0.166  66.1 -0.21 2.61 2.09  -0.01   8.40~   11  8Ø12
Peso del acero en estructura   1293 kg   ( 79.2 kg/m3)
Volumen de hormigon              16.32 m3

nº Axil Mo  Ex Mom         Espera                      Zapata              Acero  (kg)
     kN mkN mm     cmxcmx cm                   cmx cmx cm                  Ena Zap Total
__________________ _________________________  __________________________   _____________
 1  245  10 40  10 80x80x180  8Ø12 eØ 8 c/15  106x106x 40   6Ø12 x  6Ø12    38    3   42   Rigida
 2 1323  13 43  52 85x85x172 10Ø14 eØ 8 c/15  228x228x 48  12Ø20 x 12Ø20    55   38   94   Rigida
 3  591 239 43 239 85x85x178 18Ø20 eØ 8 c/15  212x212x 42  11Ø20 x 11Ø20   165   32  197   Rigida
Peso de acero incluso cimentacion 1626 kg
Volumen de hormigon total    24.83 m3    cuantia =  65.47 kg/m3

 

                             HIPOTESIS NUM.2
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
      Coordenadas       DESPLAZAMIENTOS DE NUDOS              Fuerzas en nudos
 Nudo   x       y    Direc. x  Direc. y         Giro         Fx     Fy      Mf
        m.      m.    m.          m.         rad.  Grados      T.     T.   m.T.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
 1     0.00    0.00  0.00000   0.00000   0.00000    0.000    0.00  0.00    0.00
 2     5.00    0.00  0.00000   0.00000   0.00000    0.000    0.00  0.00    0.00
 3    13.00    0.00  0.00000   0.00000   0.00000    0.000    0.00  0.00    0.00
 4     0.00    4.00 -0.00087  -0.00021   0.00036    0.021    0.00  0.00    0.00
 5     5.00    5.92 -0.00038  -0.00158   0.00085    0.049    0.00  0.00    0.00
 6    10.02    7.85  0.00112  -0.00594  -0.00123   -0.071    0.00  0.00    0.00
 7    13.00    6.01  0.00429  -0.00063  -0.00138   -0.079    0.00  0.00    0.00
 8    13.00    9.00 -0.00090  -0.00079  -0.00222   -0.127    0.00  0.00    0.00
 9    -1.00   14.40 -0.01283  -0.01429  -0.00259   -0.148    0.00  0.00    0.00
10     4.00   13.80 -0.01158  -0.00382  -0.00061   -0.035    0.00  0.00    0.00
11    13.00   13.00 -0.01124  -0.00087  -0.00223   -0.128    0.00  0.00    0.00


                             HIPOTESIS NUM.2
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
                                ESFUERZOS EN BARRAS
 i  j tB    Axil i  Corte.i    Momto.i    Axil j  Corte.j    Momto.j  m.centro  i  j
                T.      T.       m.T.        T.         T.       m.T.       m.T.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
 1  4  1   -27.08C     6.15      10.45   -27.08C     6.15      14.15      1.85  1  4
 2  5  1  -134.66C     3.45       7.26  -134.66C     3.45      13.18      2.96  2  5
 3  7  1   -52.76C    -9.60     -24.12   -52.76C    -9.60     -33.58     -4.73  3  7
 4  5  2   -15.45C   -23.08     -14.15     6.81C    34.89      44.78     -9.10  4  5
 5  6  2   -34.20C   -46.74     -57.96   -12.13C    10.68     -37.89    -28.85  5  6
 6  8  2   -14.28C   -16.79       4.06    -1.01C    17.61      -2.85    -17.16  6  8
 7  8  1   -26.34C    -1.72       3.17   -26.34C    -1.72      -8.33     -5.75  7  8
 6  7  2   -20.58C    18.34      33.83   -20.58C    18.34      30.41     -1.71  6  7
 5 10  3   -44.10C     0.00       0.00   -44.10C     0.00       0.00      0.00  5 10
 8 11  1   -10.28C     5.55      11.18   -10.28C     5.55      11.03     -0.08  8 11
 9 10  2     0.00T     0.00       0.00    -2.30T    19.18      48.34     12.09  9 10
10 11  2     7.69T   -23.85     -48.34     4.62T    10.73     -11.03    -20.37 10 11
 
Hipotesis 2
 i   j sen(a) cos    a.a    L   Area    Iner   Vol      Peso   b  h
                   grados   m.   cm²     cm4   m.³       T.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
 1  4 -1.00  0.00  -90.00  4.00 2100  857500  0.84     2.02 r 30 70
 2  5 -1.00  0.00  -90.00  5.92 2100  857500  1.24     2.98 r 30 70
 3  7 -1.00  0.00  -90.00  6.01 2100  857500  1.26     3.03 r 30 70
 4  5 -0.36 -0.93  -21.01  5.36 3200 1706667  1.71     4.11 r 40 80
 5  6 -0.36 -0.93  -21.03  5.38 3200 1706667  1.72     4.13 r 40 80
 6  8 -0.36 -0.93  -21.10  3.19 3200 1706667  1.02     2.45 r 40 80
 7  8 -1.00  0.00  -90.00  2.99 2100  857500  0.63     1.51 r 30 70
 6  7  0.53 -0.85   31.69  3.50 3200 1706667  1.12     2.69 r 40 80
 5 10 -0.99  0.13  -82.77  7.94 1800       0  1.43     3.43 ra 30 60
 8 11 -1.00  0.00  -90.00  4.00 2100  857500  0.84     2.02 r 30 70
 9 10  0.12 -0.99    6.84  5.04 3200 1706667  1.61     3.87 r 40 80
10 11  0.09 -1.00    5.08  9.04 3200 1706667  2.89     6.94 r 40 80
                                             ¯¯¯¯¯¯¯¯¯¯¯¯¯¯
                                             16.32    39.18


Hipotesis 2
Caracteristicas de los materiales
Hormigon  fck=  25 N/mm2   fcd = fck*100*0.9/cSh =   1500 T/m2
Acero HA  fyk= 500 N/mm2   fyd = fyk*100/cSa    =  43478 T/m2
-----------------------------------------------------------------------------
    Pilar con armadura simetrica en los cuatro lados
mu=M/b/h^2/fcd   v=N/b/h/fcd   w = (a1+a2*mu)/(1-a3*delta) r=40 mm
Area minima = 4*b*h/1000   area=fcd*w*b*h/fyd
Jacenas: U=0.85*fcd*b*d    v=U*d*0.375

 i  j  bxh     N    M    mu     v     x.a   a1   a2   a3     w     Area dis
      cm cm    T   mT                                               cm2  cm
 i  j                    U      v    UT     UC       aT     aC    nrT    nrC      ____________________________________________________________________________
10 11 40 80  12.3 65.7  387.6 110.9  99.21   0.00  27.38   0.00 14Ø16
             12.3 15.0               20.26   0.00   6.72   0.00  4Ø16
             12.3 37.5               52.94   0.00  14.61   0.00  8Ø16

 9 10 40 80   3.7  0.0  387.6 110.9   0.00   0.00   6.72   0.00  4Ø16
              3.7 65.7               99.21   0.00  27.38   0.00 14Ø16
              3.7 22.2               30.46   0.00   8.41   0.00  5Ø16
 8 11 30 70  16.4 17.9  0.129 0.083  82.8 -0.17 2.55 2.04  0.18  8.43      11  8Ø12
 5 10 30 60  70.6  1.6  0.036 0.951  51.3 -0.11 2.91 2.01 -0.01 7.20~ª2.29 11  8Ø12
 6  7 40 80  32.9 46.0  387.6 110.9  66.20   0.00  18.27   0.00 10Ø16
             32.9 41.4               58.89   0.00  16.25   0.00  9Ø16
             32.9  3.2                4.17   0.00   6.72   0.00  4Ø16
 7  8 30 70  42.1 13.3  0.096 0.212  12.3 -0.25 2.66 2.13   0.01   8.40~   11  8Ø12
 6  8 40 80  22.8  6.5  0.027 0.076  75.5 -0.19 2.58 2.06  -0.13  12.80~   13 10Ø14
 5  6 40 80  54.7 78.8  387.6 110.9 123.34   0.00  34.04   0.00 17Ø16
             54.7 51.5               75.08   0.00  20.72   0.00 11Ø16
             54.7 53.1               77.61   0.00  21.42   0.00 11Ø16

 4  5 40 80  24.7 19.2  387.6 110.9  26.20   0.00   7.23   0.00  4Ø16
             24.7 60.9               90.76   0.00  25.05   0.00 13Ø16
             24.7 21.3               29.10   0.00   8.03   0.00  4Ø16
 3  7 30 70  84.4 53.7  0.575 0.633  32.6 -0.28 2.77 2.36   1.52
      35 75             0.401 0.472  72.3 -0.32 2.75 2.28   0.89  50.69    ª1.39  6 18Ø20
 2  5 30 70 215.5 21.1  0.222 1.590
      35 75               0.155 1.187  87.5  0.07 3.01 1.56   0.58  33.30  ª1.37  8 14Ø20
 1  4 30 70  43.3 22.6  0.163 0.218  18.4 -0.25 2.66 2.13   0.21   9.52    11  8Ø14
Peso del acero en estructura   1482 kg   ( 90.8 kg/m3)
Volumen de hormigon              16.32 m3

nº Axil Mo  Ex Mom         Espera                      Zapata              Acero  (kg)
     kN mkN mm     cmxcmx cm                   cmx cmx cm                  Ena Zap Total
__________________ _________________________  __________________________   _____________
 1  324 104 40 104 80x80x180  8Ø14 eØ 8 c/15  161x161x 40   9Ø14 x  9Ø14    47   10   57   Rigida
 2 1448  73 43  73 85x85x168 14Ø20 eØ 8 c/15  242x242x 52  13Ø20 x 13Ø20   131   45  175   Rigida
 3  608 241 43 241 85x85x176 18Ø20 eØ 8 c/15  218x218x 44  11Ø20 x 11Ø20   165   33  198   Rigida
Peso de acero incluso cimentacion 1913 kg
Volumen de hormigon total    26.16 m3    cuantia =  73.10 kg/m3

Estructuras de paraboloides hiperbolicos

Estructura combinacion de tres parabolides hiperbolicos

Programa de calculo 3D. Apoyos de la estructura.

Otros artículos del manual del programa "Estructuras 3D"

Los datos de entrada

 Cargas en los nudos

El programa de cálculo "Estructura 3D CAL" define los nudos de apoyos mediante cuatro elementos por nudos : el numero o denominación del nudo y tres coeficientes de coacción  de movimiento que también se llaman coeficientes de muelle y otros tres coeficientes de coacción de giro. Si la estructura tiene solo dos dimensiones habrá en consecuencia solo dos coeficientes de coacción.


Si el nudo tiene libertad de movimiento en alguna dirección x, y o z, este coeficiente sera igual a la unidad.
Si el nudo es completamente rígido y sin movimiento en ninguna dirección el coeficiente sera igual a  cero.
Si el nudo tiene cierta elasticidad el coeficiente tendrá un valor diferente de 0 y de 1.

Cuando el coeficiente es cero en la diagonal de la matriz se pone un valor muy alto 10^20 y en el caso de nudo elástico aparecerá en la diagonal de la matriz el valor de esa elasticidad.

Todos los casos que pueden presentarse son estos:
1º) Estructura articulada de 2 dimensiones:  Nº  C1  C2
2º) Estructura articulada de 3 dimensiones:  Nº  C1  C2  C3
3º) Estructura rígida de 2 dimensiones:         Nº  C1  C2 G1 
4º) Estructura rígida de 3 dimensiones:         Nº  C1  C2  C3  G1  G2  G3

Los giros que se imponen a los nudos se expresaran en radianes y las constantes elásticas de giro se indicaran en la unidad elegida por radian de giro.

Ejemplo:
Supongamos una celosía de 2 dimensiones con dos apoyos extremos y un tirante elástico entre ellos, 

Datos:
Área del tirante entre apoyos......... A : 48 cm2
Longitud del tirante ...................... L : 48 m.
Modulo de elasticidad .................. E : 21·10^6

El coefiente de muelle del apoyo elástico sera:
Kx = E·A/L =   21·10^6 · 48 ·10^-4  /  48  =  2100 T/m

En el programa pondremos como datos de apoyos 1 y 20:

1  2100  0  0 ,  20  0  0  0 

En el apoyo 1 el coeficiente de coacción en la dirección x es 2100, el coeficiente de coacción en la dirección y es 0 y el coeficiente de coacción en la dirección z es 0.  En el apoyo 20 los tres coeficientes son de valor cero pues ese apoyo se considera completamente rígido, es decir sin movimiento alguno.

Colapso de estructura de hormigon armado (Rana Plaza de Bangladesh)

Ecuacion parabola-rectangulo. Dominio 2

Calculo de Nc, resultante del axil de compresion en seccion de hormigon armado, en el Dominio 2, es decir, cuando la deformacion de la fibra mas comprimida del hormigon es menor de 0.002

COMPROBACION DE PIEZA DE H.A. sometida a flexion esviada

COMPROBACION DE PIEZA DE H.A. sometida a flexion esviada 23

RIGIDECES RELATIVAS PARA CALCULO DE PORTICOS

Longitud  Ancho x Canto  Mo.Inercia  Rigidez           Rigidez relativa a una pieza de 300 x
   m       cm      cm       m^4        m3                30x30     40x40    50x50    60x60  
                                               Rig.x1000  0.2       0.7      1.7      3.6   
____________________________________________________________________________________________

Cálculo rápido de pórticos: momentos flectores

Los gráficos siguientes indican los coeficientes que necesitamos para predimensionar un portico plano. En primer lugar tenemos que multiplicar la carga por metro lineal de la jácena por su luz al cuadrado. Por ejemplo, si la carga por metro lineal de la jácena es de 3 T y la luz es de 4 m, calculamos  el producto de la carga por la luz al cuadrado: 3 x 4 x 4 = 48. Este resultado se divide por 9 o por 10 o por el coeficiente que corresponda según este gráfico procedente de la instrucción española EH-91:

Tenemos dos series de gráficos: la serie de la izquierda para pórticos de solo dos vanos y a la derecha para un caso más general de varios vanos.

De arriba hacia abajo se representan pórticos mediante el eje de las jácenas y el principio del pilar superior e inferior.

Cada uno de esos pórticos se diferencia de otro por la rigidez relativa entre la jácena y los pilares. Esa rigidez relativa está marcada entre paréntesis. Por ejemplo, el pórtico más abajo de la serie de la izquierda, es un pórtico con jácenas muy poco rígidas respecto de sus pilares, es decir pilares muy gruesos en relación a la jácena. Si nos vamos a la parte alta del gráfico, primero tenemos una jácena de cubierta, sin pilares encima e inmediátamente debajo una jácena muy rígida (3) respecto a sus pilares (1).

Con los criterios explicados debemos elegir los coeficientes. Ahora bién si no precisamos grán esáctitud, pues se trata de un procedimiento de predimensionado, no de dimensionado definitivo, podemos simplificar esas tablas eliminando  los casos menos desfavorables. 

Veamos un ejemplo con los graficos anteriores: 

Un pórtico de 4 jácenas con vigas y pilares de rigidez similar, elegimos  los coeficientes de la serie de la derecha y de la viga donde las rigideces se indican con un (1) igual que los pilares (1), los coeficientes serian:

14, para el momento positivo de las jácenas mas extremas

18, para el momento positivo de las jácenas centrales

18, para el momento negativo en los nudos extremos

10, para el momento negativo en los nudos centrales.

35, para el momento de los pilares extremos.

Asi que, si como en el caso anterior la carga por la luz al cuadrado es 48, los momentos flectores seran:

Momento positivo de las jácenas extremas: 48/14 = 3,43 mT 

Momento positivo de las jácenas centrales: 48/18 = 2,67 mT 

Momento negativo de los nudos extremos:  48/18 = 2,67 mT 

Momento negativo de los nudos centrales:  48/10 = 4,80 mT 

Momento en pilares extremos                     :  48/35 = 1,38 mT

En caso de que las cargas no estuvieran mayoradas debemos mayorar estos resultados conveniéntemente, para con ellos predimensionar las jácenas y los pilares.

Cuantías mínimas en pilares de hormigón armado